I recently painted my house, and while purchasing paint from Sherwin Williams I was nerd sniped by their logo — a globe-sized paint can pouring down from space, accompanied by the phrase “cover the earth”. I immediately wanted to know several things: How big is that can? Would it really cover the earth? How much paint would actually be needed to cover the earth? So of course I set aside an hour or so to work through the math.

The first thing I did was calculate the size of the paint can. I measured the diameter of the Earth in pixels, and used the known value for Earth’s diameter (3958.8 miles) to find a conversion factor from pixels to miles. Then I could measure the dimensions of the paint can in pixels, and convert back to miles. I found that the can was 2468.1 miles tall, with a diameter of 2694.9 miles (or a radius of 1347.2 miles, since that’s the figure used in the calculations). For a cylinder, the formula for volume is $V=\pi r^2h$. With these values, the result is a volume of 22.43 million cubic miles, or 2.469×10¹⁹ gallons. That’s a lot of paint! In fact, it’s about $\frac{1}{14}$ the volume of all of the earth’s oceans.

Is it enough to actually cover the earth though? To answer that, we need to know the surface area of the earth. We’ll just assume earth is a featureless sphere here, because accounting for any of the irregularities on the earth’s surface will inevitably lead to the coastline paradox, and there’s really no reason to be any more accurate since we’ll almost surely never see this much paint in one place in our lifetimes. The surface area of a sphere is calculated by $SA=4\pi r^3$, so using the same value for the diameter of the earth, we can calculate that the earth has a surface area of 196.94 million square miles. Of course, paint isn’t 2-dimensional, so we need to calculate the volume of the covering, not just the surface area it covers. To find this, we can use the same formula for the volume of a sphere, but in reverse. We know that the volume of the paint-covered earth sphere will be the volume of the earth plus the volume of the paint. From this, we can determine what the radius new of the paint-covered earth would be, then all we need to do is subtract the radius of the earth and we’re left with the raidus of the paint! I’ve attached a crudely-drawn diagram below to help explain.

$$\begin{align} V_{painted\_earth} &= \frac{4}{3} \pi r_{painted\_earth}^3 \\ V_{painted\_earth} &= V_{earth} + V_{paint} \\ \frac{4}{3} \pi r_{painted\_earth}^3 &= V_{earth} + V_{paint} \\ r_{painted\_earth} &= \sqrt[3]{\frac{3\left(V_{earth} + V_{paint}\right)}{4\pi}} \\ r_{paint} &= r_{painted\_earth} - r_{earth} \\ r_{paint} &= \sqrt[3]{\frac{3\left(V_{earth} + V_{paint}\right)}{4\pi}} - r_{earth} \end{align}$$

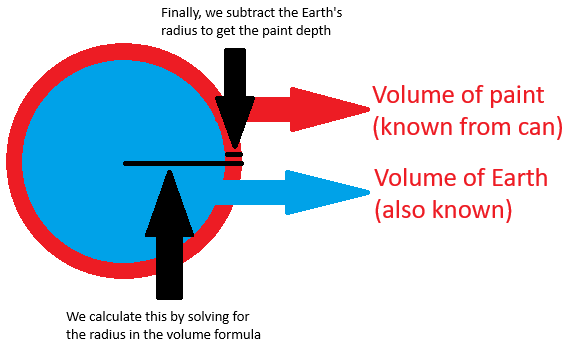
With all of that algebra out of the way, we can finally calculate just how deep the layer of paint coating the earth would be 0.1435 miles thick, or 757.72 feet, not quite deep enough to cover the Eiffel Tower which stands at 984 feet. Just how deep is that? Take a look for yourself!

It seems the folks at Sherwin Williams have overestimated the size of the paint bucket needed to cover the earth. How much paint would we actually need? If we settle on a layer thickness, we can again make use of the sphere volume formula to reverse-engineer what the paint volume would be as follows:

$$\begin{align} V_{paint} &= V_{painted\_earth} - V_{earth} \\ V_{painted\_earth} &= \frac{4}{3} \pi r_{painted\_earth}^3 \\ r_{painted\_earth} &= r_{paint} + r_{earth} \\ V_{painted\_earth} &= \frac{4}{3}\pi\left(r_{paint} + r_{earth}\right)^3 \\ V_{paint} &= \frac{4}{3}\pi\left(r_{paint} + r_{earth}\right)^3 - V_{earth} \end{align}$$

Easy enough! If we set $r_{paint}$ to a very small value, say 1mm, we run into trouble though — 1mm is way too small relative to the rest of the sizes we’re working with so far, so most calculators just round it down to zero. To solve this issue, I converted all of my units to millimeters, and switched to using an arbitrary-precision decimal library to make sure I keep full precision on all of my calculations. The final result I calculated was 5.101×10²⁰ cubic millimeters of paint, which equates to 1.348×10¹⁴ gallons. That’s just one ten thousandth of the paint in the can on the logo! If the resulting can had the same ratio of height to diameter as the can in the logo, it would be reduced to “just” 28082 feet tall, which is about the same height as Mount Everest (29000 feet).

What if we set $r_{paint}$ to the thickness of a single pigment particle, so we can cover the entire surface of the earth in a coating of paint exacly one particle thick? According to a source I no longer remember, a single pigment particle is around 25 microns. Following the same process as above, we can calculate that the new paint can would hold 3.37×10¹² gallons and stand at 8212.26 feet tall, 3x the height of the Burj Khalifa, the tallest building on earth.

Now there’s just one question left: how much would it cost to buy such an insane amount of paint? One gallon of exterior paint from SW ranges in price from $60 on the cheap end up to $120. I’ll settle on $100 per gallon, which makes the math very easy — we just need to increase the exponent on our volume in gallons by 2. The paint bucket in the logo then would cost 2,469 quintillion US dollars. As I’m writing this, the world bank estimates the total global GDP at $100 trillion, which means if every nation on earth dedicated their entire economy to purchasing paint, it would take 24,690,000 years to purchase all of it. The paint sized for a 1mm coating would be affordable after 134.8 years, and the 25 micron coating would be affordable after just 3.37 years!

Global GDP isn’t static though, and according to the data available from the world bank, it grows at a rate of about 3.47% per year. If we factor in this growth (which is already adjusted for inflation, so we can keep the price of paint fixed), how much faster could we afford the big can? We can model this growth with a geometric series. The sum of the terms of a geometric series has a very convenient closed-form solution, so this calculation should be somewhat straightforward as well. Where $n$ is the number of years it will take to reach our target amount of money $T$, we can calculate the following:

$$\begin{align} T &= \sum_{n=0}^{n} {1.0347\times10^{14}} \\ T &= 10^{14}\left(\frac{1.0347^n-1}{1.0347-1}\right) \\ \frac{T\left(1.0347-1\right)}{10^{14}}+1 &= 1.0347^n \\ \log_{1.0347}\left({\frac{T\left(1.0347-1\right)}{10^{14}}+1}\right) &= n \end{align}$$

Inputting the cost of our giant paint can for T, we get a much more reasonable 400 years! Maybe there’s hope that someday our great great grandchildren could actually coat the entire earth in paint. Until then, I’m going to keep procrastinating painting my own house.